МОДЕЛЬ ПОДГОТОВКИ МЛАДШИХ ШКОЛЬНИКОВ К УЧАСТИЮ В МАТЕМАТИЧЕСКИХ КОНКУРСАХ, ИССЛЕДОВАТЕЛЬСКИХ ПРОЕКТАХ И УЧЕНИЧЕСКИХ КОНФЕРЕНЦИЯХ
Козлова Мария Алексеевна,
студент,
Научный руководитель: Уткина Т.И.,
доктор педагогических наук, профессор
Орский гуманитарно-технологический институт
(филиал) Оренбургского государственного университета
Аннотация: Представляется методика диагностирования уровня готовности младших школьников к участию в математических конкурсах, исследовательских проектах и ученических конференциях. Раскрывается содержание методики. Выявляется компонентный состав готовности к участию в математических конкурсах, исследовательских проектах и ученических конференциях.
Ключевые слова: модель, математический конкурс, исследовательский проект, ученическая конференция.
В данной работе предъявлены результаты исследования по разработке методики диагностирования уровня развития готовности младших школьников к участию в математических конкурсах, исследовательских проектах и ученических конференциях.
Актуальность проблемы определяется социальным запросом, сформулированным в ФГОС НОО, требованиями профессионального стандарта «Педагог», а также текущей ситуацией в школах.
В основу создания методики были положены результаты проведенного теоретического исследования по выявлению содержания и компонентного состава готовности младших школьников к участию в математических конкурсах, исследовательских проектах и ученических конференциях: умения анализировать результаты математических конкурсов и конференций, не владение основными приемами решения математических заданий; умение осуществлять собственную учебную деятельность, самостоятельно планирует деятельность, под руководством учителя верно выполняет задания математических конкурсов и конференций; умение четко, последовательно осуществляет решение математических заданий, самостоятельно и правильно выполняет задания математических конкурсов и конференций.
Методологической основой проектирования выявленного компонентного состава умений участия в математических конкурсах, исследовательских проектах и ученических конференциях являлись труды Б.П. Гейдман [1], А.О. Ефремушкиной [2], М.И. Моро [3], Б.П. Гейдмана [4], Н.С. Лейтеса [5], А.И. Савенкова [6], Л.П. Стойловой [7]. В данной работе под моделью понимается созданный объект в виде таблицы, которая отражает в более простом и обобщенном виде структуру, свойства, взаимосвязи и отношения между элементами этого объекта.
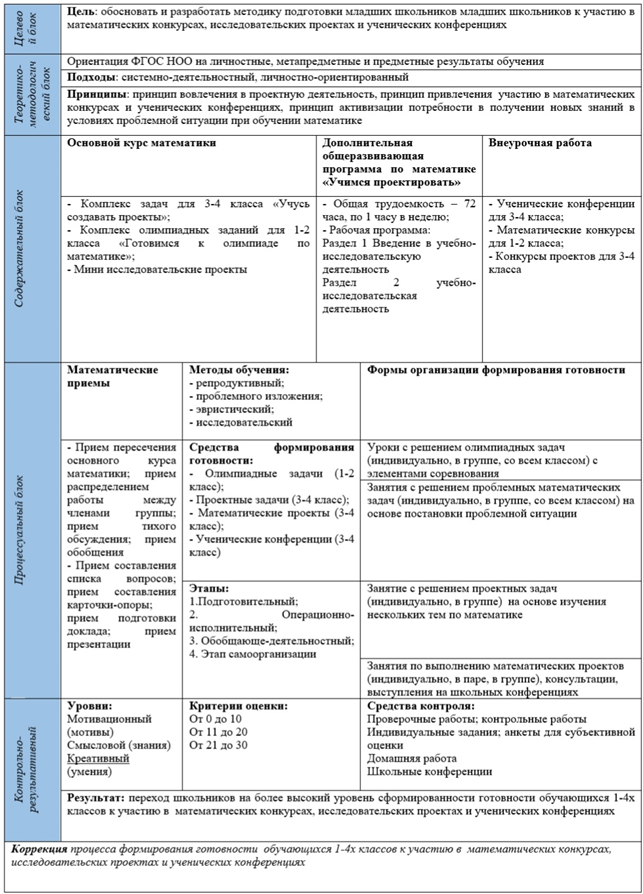
Разработанная модель включает пять блоков (см. рис. 1) (целевой, теоретико-методологический, содержательный, процессуальный, контрольно-результативный).
Целевой блок ориентирован на подготовку младших школьников младших школьников к участию в математических конкурсах, исследовательских проектах и ученических конференциях.
Методический блок раскрывает подходы (системно-деятельностный, личностно и практико-ориентированный), принципы (принцип вовлечения в проектную деятельность, принцип привлечения к участию в математических конкурсах и ученических конференциях, принцип активизации потребности в получении новых знаний в условиях проблемной ситуации при обучении математике), и ориентированность на требования ФГОС относительно личностных, предметных и метапредметных результатом обучения.
В содержательном блоке раскрываются направления подготовки младших школьников младших школьников к участию в математических конкурсах, исследовательских проектах и ученических конференциях через основной курс математики, дополнительную общеразвивающую программу «Учимся проектировать» (курс по выбору) и внеурочную работу (Ученические конференции Математические конкурсы).
Подготовка к участию в математических конкурсах, исследовательских проектах и ученических конференциях через основной курс математики модель рассматривает посредством использования комплекса задач «Учусь создавать проекты», комплекса олимпиадных заданий «Готовимся к олимпиаде по математике», а также мини-исследовательские проекты.
Общая трудоемкость дополнительный общеразвивающей программы составляет 72 часа и включает следующие разделы: раздел 1 «Введение в учебно-исследовательскую деятельность», раздел 2 «Учебно-исследовательская деятельность».
Диагностический блок выявляет три уровня развития готовности младших школьников младших школьников к участию в математических конкурсах, исследовательских проектах и ученических конференциях и раскрывает методику обработки результатов, полученных в ходе реализации содержательного блока. Мотивационный уровень (от 0 до 10 баллов) – состояние тревоги и неуверенности в себе, непонимание смысла математических конкурсов и конференций. Отсутствие знаний в области математических конкурсов и конференций. Отсутствие умения анализировать результаты математических конкурсов и конференций, не владение основными приемами решения математических заданий.
Смысловой уровень (от 11 до 20 баллов) – понимание смысла математических конкурсов и конференций, но недостаточная мотивация к усовершенствованию своих знаний. Правильное, но недостаточно четкое представление о математических конкурсах и конференциях.
рис. 1. Модель развития у младших школьников умений графического моделирования в процессе обучения решению текстовых задач на движение
Умение осуществлять собственную учебную деятельность, самостоятельно планирует деятельность, под руководством учителя верно выполняет задания математических конкурсов и конференций.
Креативный уровень (от 21 до 30 баллов) – высокий уровень познавательной мотивации, адекватное представление о роли математических конкурсов и конференций, потребность в усовершенствовании своих умений. Знание достаточного количества материала в области математики, умение их грамотно применить в определенной ситуации. Умение четко, последовательно осуществляет решение математических заданий, самостоятельно и правильно выполняет задания математических конкурсов и конференций.
Результативный блок позволяет делать вывод о переходе обучающихся на более высокий уровень готовности младших школьников младших школьников к участию в математических конкурсах, исследовательских проектах и ученических конференциях.
Представленная модель прошла апробацию на базе МОАУ СОШ №25 г. Орска и внутривузовской конференции, в ходе которой доказана эффективность разработанной модели.
ЛИТЕРАТУРА:
- Гейдман Б. П. Подготовка к математической олимпиаде. Начальная
- Ефремушкина А.О. Школьные олимпиады для начальных классов / А.О. Ефремушкина. – Изд.10-е. Ростов н-Д: Феникс, 2009. 186 с.
- Моро М.И., Пышкало А.М. Методика обучения математике в 1-3 классах / И.М. Моро, А.М. Пышкало. — М.: Просвещение, 1975.
- Подготовка к математической олимпиаде. Начальная школа. 2-4 классы / Б. П. Гейдман, И. Э. Мишарина. — 3-е изд., испр. — М.: Айрис-пресс, 2007. — 128 с.
- Психология одаренности детей и подростков/ Под ред. Н.С. Лейтеса. М.: Издательский центр «Академия», 1996. — 416 с.
- Савенков А.И. Одаренные дети в детском саду и в школе / А.И. Савенков — Москва, — 2000 г.
- Стойлова Л. П. Математика: Учебник для студентов высших пед. учеб. Заведений / Л.П. Стойлова. — М.: Академия, 2007.
Здравствуйте, Мария!
Спасибо за поднятую тему. Действительно, проекты, особенно по математике, являются важным компонентом в школьной жизни. Мне очень понравились предложенные этапы подготовки младших школьников. Я считаю, что у Вас получилось кратко и продуктивно дифференцировать уровни подготовки. Обязательно попробую применить на практике Вашу методику.
Доброго времени суток!
Благодарю за оценку проделанной работы!