РЕШЕНИЕ ЗАДАЧ С ПАРАМЕТРАМИ В СРЕДЕ «GEOGEBRA»

Статья опубликована в рамках: Международной научно-практической интернет-конференции «Актуальные проблемы методики обучения информатике и математике в современной школе» (Россия, г.Москва, МПГУ, 22 — 26 апреля 2019г.)

РЕШЕНИЕ ЗАДАЧ С ПАРАМЕТРАМИ В СРЕДЕ «GEOGEBRA»

Сажнева Анна Михайловна,
Балашовский институт (филиал)
ФГБОУ ВО «СГУ им. Н. Г. Чернышевского»,
г. Балашов

Аннотация: В статье рассматривается возможности использования пакета GeoGebra при подготовке учащихся к решению задач с параметрами. Целью данной статьи является определение условий введения пакета GeoGebra в учебный процесс, для обеспечения наглядности и эффективности обучения.

Ключевые слова: компьютерные программы, GeoGebra.

Федеральный государственный образовательный стандарт [1] предъявляет новые требования к результатам обучения предметной области «Математика и информатика», они связаны с овладениями приёмов использования информационных образовательных технологий, которые помогут активизировать учебный процесс. Это говорит нам о том, что невозможно обойтись без методов современного обучения, и в частности различных технологий.

В настоящее время существуют программы, которые можно использовать на уроках математики, такие как, Euclidea, Живая математика, Geometry Pad и др.

Одной из таких бесплатных, кроссплатформенных динамических программ является GeoGebra. Она включает в себя следующие разделы: алгебру, геометрию, таблицы, графы, статистику и арифметику, что говорит о широких возможностях данной программы. Это позволяет ученикам быстро, наглядно и точно выполнить любые построения и операции, а именно: геометрические построения, построение графиков, вычисление корней, экстремумов и интегралов и т.д.

Все эти возможности позволяют внедрить это приложение для решения задач с параметрами. В курсе ОГЭ это задание под номером 23, а в материалах ЕГЭ это задание под номером 18. При выполнении таких задач очень часто требуется построить график функции и провести его исследовании. Использование платформы GeoGebra позволит учащимся проконтролировать правильность хода решения задачи.

В качестве примера рассмотрим использование GeoGebra при решении задания № 18 из ЕГЭ [2].

Задача. Найти все значения параметра a, при каждом из которых уравнение $ax+\sqrt{3-2x-x^2}=4a+2$ имеет единственный корень.

Решение. Перепишем уравнение в виде $\sqrt{3-2x-x^2}=-ax+4a+2$

и рассмотрим график левой и правой части. Количество решений исходного уравнения будет зависеть от количества точек пересечения графиков $f(x)= \sqrt{3-2x-x^2}$ и $g(x)=-ax+4a+2$ .

Найдем область определения функции $y = \sqrt{3-2x-x^2}$ .
D(y)=[-3;1].

И проведем некоторые преобразования с функцией.
$(x+1)^2+y^2=4$

Исходя из этого, можно сделать вывод, что графиком функции $f(x) = \sqrt{3-2x-x^2}$ является полуокружность с центром в точке (-1;0) и радиусом 2.

Уравнение $g(x)=-ax+4a+2$ задает семейство прямых, после преобразования получим: y=-a(x-4)+2. Можно заметить, что семейство проходит через точку (4;2) с угловым коэффициентом, который равен -a.

На основании изложенного можно сделать вывод о том, что уравнение имеет единственный корень, если прямая касается полуокружности, либо пересекает её в единственной точке.

Для наглядности построим динамический чертеж в программе GeoGebra. Для этого выполним следующую последовательность действий:

набираем в строке ввода функцию $g(x)=-ax+4a+2$ ;
при помощи инструмента «Ползунок» на панели инструментов добавляем ползунок, который может менять свое значение от –5 до 5, с шагом 0,001 (значения выбраны случайным образом и могут меняться в зависимости от решения);
набираем в строке ввода функцию $f(x) = \sqrt{3-2x-x^2}$

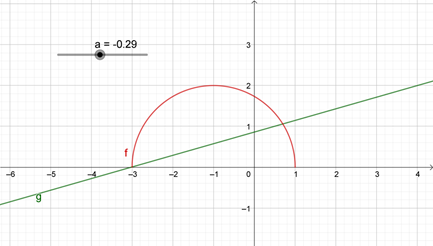
В результате получим рис.1.

Рис.1.

Изменяя значение ползунка, мы видим, что касательная к полуокружности имеет угловой коэффициент, равный 0, а при a>0 прямая не имеет общих точек с полуокружностью.

Возможен случай, когда прямая пересечет окружность в двух точках, если прямая будет проходить через точку (–3;0) и получим рис.2.

Рис. 2.

Подставим точку (-3;0) и получим, что коэффициент $a=-\frac{2}{7}$ . Меняя значение ползунка, можно заметить, что уравнение будет иметь единственное решение до того момента, когда прямая будет проходить через точку (1;0) (см. рис. 3). Подставим точку и получим, что $a=-\frac{2}{3}$ .

Рис. 3.

Поэтому исходное уравнение будет иметь единственное решение при $- \frac{2}{3} \leqslant a<-\frac{2}{7}$ , а также при a=0.

Для того чтобы учащимся было более понятно решение данной задачи, то на этапе подготовки следует ввести решение таких заданий, используя пакет Geogebra для проверки правильности решения. Однако стоит отметить, что программа не должна заменить решение таких задач, а только помочь разобраться с материалом. В программе GeoGebra все чертежи «оживают», их легко можно изменить. Она позволяет отработать такие навыки как: построение графиков функций, нахождение области определения, а также она позволяет решать задачи с параметром не мысленно, а наглядно. Что касается задач с параметром, то обычно они трудны для учеников и требуют много времени, однако, если проводить построения с помощью приложения «GeoGebra», то построения становятся точными и быстрыми.
ЛИТЕРАТУРА:

Федеральный государственный образовательный стандарт. URL: https://fgos.ru/LMS/wm/wm_fgos.php?id=sred (Дата обращения: 10.03.19)
ЕГЭ, задание 18. URL: https://ege.sdamgia.ru/test?theme=265 (Дата обращения: 10.03.19)