ОБУЧЕНИЕ ДОКАЗАТЕЛЬНЫМ РАССУЖДЕНИЯМ ПО ПОИСКУ РЕШЕНИЯ ЗАДАЧ МЕТОДОМ ПЕРЕНОСА

Аннотация:  В работе рассматривается конструирование модели ориентировочной основы проектирования доказательных рассуждений по поиску решений геометрических задач методом переноса. Выделяются виды геометрических задач, решаемых методом переноса.
Ключевые слова: модель, ориентировочная основа, метод переноса.

Актуальность данной темы исследования определяется требованиями профессионального стандарта «Педагог» и ФГОС общего образования.

В основу обучения доказательным рассуждениям по поиску решения задач методом переноса положены результаты ранее проведенного теоретического исследования по созданию модели ориентировочной основы по поиску решения геометрических задач методом переноса.

Методологической основой проектирования модели ориентировочной основы обучения доказательным рассуждениям положены труды П.Я.Гальперина [3]. В данной работе под моделью понимается созданный объект  в виде алгоритма, схемы, ориентировочной основы для поиска решения задач методом переноса.

С целью определения видов задач, решаемых методом переноса был проведён анализ учебника Л.С. Атанасяна [2], который  позволил  выделить следующие три типа задач, решаемых методом переноса: задачи на построение; задачи на доказательство; задачи с фигурами,  которые являются соответствующими в переносе, в которых может  быть использован перенос.

На основе анализа их решений  была разработана  модель ориентировочной основы проектирования доказательных рассуждений по поиску решения геометрических задач методом переноса. Модель ориентировочной основы доказательных рассуждений включает пять блоков: изучение содержания задачи, анализ, выбор преобразования,  обоснование свойств, доказательный блок.

Блок изучения содержания задачи направлен на уяснение взаимного расположения данных (данных и искомых) точек или фигур (или их частей и элементов).

В блоке анализа (поиска решения) – осуществляется обоснование возможности решения задачи методом переноса,  составляется (при необходимости) эскиз, устанавливаются связи между данными задачи и желаемыми (точками, фигурами, их элементами). или свойства), чтобы выбрать (задать) геометрическое преобразование, которое позволит обосновать наличие тех или иных отношений между объектами (точками, формами).

В блоке выбора преобразования — указать (или выполнить) выбранное преобразование, чтобы один объект перешел в другой (или создать вспомогательную фигуру).

В блоке на обоснование свойств — обосновывается наличие указанной связи между объектами, используя свойства выбранного преобразования.

В блоке на доказательство — в задаче на построение, если необходимо, преобразовать вспомогательную фигуру в требуемую и провести доказательство, как в блоке на обоснование свойств (а также исследование).

Пример применения ориентировочной основы для решения конкретной задачи.

Ученики 7-8 классов сначала испытывают значительные трудности с подходом к задаче на построение. Поэтому необходимо научить стандартной процедуре решения: анализ→построения→доказательство→исследование.

Задача.

Построить трапецию по заданным её сторонам.

Подробнее: требуется построить трапецию так, чтобы её основания были соответственно равны данным отрезкам a и b (a>b), а боковые стороны были соответственно равны двум данным отрезкам c и d (cd).

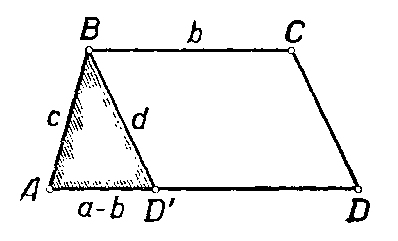
Анализ. Допустим, что ABCD– искомая трапеция, AB=c, CD=d, AB и CD – боковые стороны, причём AD – её большее основание, BC — меньшее основание.

Рисунок

Представим себе перенос, определяемый вектором . Затем (см. Рис.) сторона CD преобразуется в отрезок BD´. Треугольник АBD´ может быть построен, так как все стороны его известны. Чтобы построить искомую трапецию, осталось  перенести отрезок BD´ переносом на вектор , длина которого известна и который направлен одинаково с вектором .

Построение.

1) Построим треугольник ABD´ по сторонам AB=c, ВD´=d, и AD´=a – b.
2) Построим образ ВD´ в переносе на вектор, длина которого b и сонаправлен с лучом AD´.
3) ABCD – искомая трапеция.

Доказательство. AB=c, ВС= b по построению; AD= AD´+ D´D= AD´+ ВС=a – b + b = a. CD=BD´. [1, стр. 94]

Исследование. Первое построение выполнимо при условии:
d – c < a – b < d + c.

При этом условии все остальные этапы построения выполняются однозначно. Отметим также, что треугольник ABD´, а следовательно, и трапеция ABCD определяются условиями задачи однозначно до равенства. Следовательно, при условии d – c < a – b < d + c задача имеет единственное решение. Если это условие не выполняется, то задача не имеет решения. [1, стр. 95]

Составим ориентировочную модель для оформления решения задачи:

• Допустим, что фигура построена и нужно выбрать направляющий вектор, с помощью которого будет происходить перенос.
• Берем точки или прямые и с помощью направляющего вектора совершаем перенос.
• Обосновываем наличие указанного отношения между объектами с помощью свойств параллельного переноса.
• При необходимости преобразуйте вспомогательную фигуру в искомую и проведите доказательство, затем мы проведем исследование на количество решений этой задачи.

С целью более полного освоения учащимися умственных действий, необходимых для решения задач методом переноса, был  разработан математический конкурс «Метод переноса при решении геометрических задач» для учащихся 8-9 классов.

Достоинством созданной модели ориентировочной основы решения задач методом переноса является то, что учащиеся могут пользоваться ею самостоятельно.

1. Аргунов Б.И. Балк М.Б. Геометрические построения на плоскости. М., 1957. 266 с.
2. Атанасян Л. С. Геометрия. 7—9 классы: учеб. для общеобразоват. учреждений / В. Ф. Бутузов, С. Б. Кадомцев и др. — 20-е изд. — М.: Просвещение, 2010. 384 с.
3. Гальперин П. Я. Методы обучения и умственное развитие ребенка. — М., 1985.
4. Гордин Р. К. Геометрия. Планиметрия. 7–9 классы. — 3-е изд., испр. — М.: МЦНМО, 2006.  416 с.