ЗАДАЧНЫЙ ПОДХОД КАК ОСНОВА ЭФФЕКТИВНОГО ОБУЧЕНИЯ ШКОЛЬНИКОВ МАТЕМАТИКЕ

Аннотация. В статье актуализируется роль задачного подхода в организации эффективного обучения математике. Представлена общая характеристика эффективной задачной системы. Приведен пример системы задач, которая может быть использована на этапе изучения нового материала с целью повышения эффективности обучения.

Ключевые слова: эффективное обучение, задача, система задач, задачный подход.

Эффективность любой системы – понятие, обозначающее тот уровень ее функционирования, который соответствует наиболее оптимальному и максимальному достижению целей системы, при минимальном количестве отрицательных последствий или издержек. Повышение эффективности школьного образования на современном этапе связывается с достижением комплексного образовательного результата в единстве трех его компонентов: предметного (знания, умения, предметные компетенции), метапредметного (обобщенные знания и способы деятельности, познавательная компетентность) и личностного (качества личности обучающегося, определяющие его активную жизненную позицию, позволяющие найти достойное место в обществе). Эффективность, как многокомпонентная системная характеристика процесса обучения определяется совокупностью различных компонентов [2, 4, 7 и др.], одним из которых является активность обучающихся в качестве субъектов образовательного процесса.

Активным считается такое обучение, которое строится не на передаче учителем информации, запоминании и последующем воспроизведении ее учащимися, а на самостоятельном заинтересованном овладении школьниками теоретическими знаниями и способами их применения на практике, обучение, в котором обучающийся может самореализоваться, гармонически взаимодействуя как с другими участниками образовательного процесса, так и с образовательной средой в целом. Не случайно повышение эффективности обучения педагоги связывают с использованием активных и интерактивных методов. В последнее время появилось большое количество статей, пособий, в которых рассматривается классификация активных и интерактивных методов, а также описываются особенности реализации этих методов. Однако большинство этих пособий раскрывают суть таких методов безотносительно особенностей учебных предметов, другая же часть пособий описывает применение указанных методов при изучении социально-гуманитарных дисциплин, для которых они собственно и были придуманы. Таким образом, существует необходимость такого подхода, который, вне зависимости от дисциплины, позволял бы структурировать обучение как активный мыслительно-деятельностный процесс.

Один из возможных вариантов решения указанной проблемы связан с реализаций задачного подхода, основным положением которого является утверждение о том, что освоение новых знаний, умений и навыков учащихся, а также их личностное развитие возможно осуществить на основе специально разработанной системы учебно-познавательных задач, которые обеспечивают содержательно-деятельностную основу различных учебных ситуаций, как единиц процесса обучения. Г. А. Балл по этому поводу замечает: «Руководимый педагогом процесс решения задачи, возникающие в этом процессе отношения, используемые средства и полученные результаты составляют структурную единицу процесса обучения» [1, с. 28].

В литературе (Г. А. Балл, Г. Д. Бухарова, Л. Л. Гурова, Ю. М. Колягин, В. В. Давыдов, Е. И. Машбиц, Л. М. Фридман и др.), определены основные принципы задачного подхода, психолого-педагогические аспекты включения задач в учебный процесс. Успешность реализации задачного подхода в обучении обуславливается четким представлением учителя о его структуре, принципах и условиях, в которых он должен осуществляться. При этом понятие «задача» должна рассматриваться как в общем лексическом значении – вообще что-либо, что необходимо сделать, действие, которое необходимо выполнить, так и в более узком, как некоторая словесная знаковая структура.

О функциональной многогранности задач и их роли в повышении эффективности образования можно судить по широкому спектру диссертационных исследований и научных монографий, в которых установлено, что задачи в обучении математике:

• выступают формой представления учебного содержания;
• являются средством: углубленного освоения математики, систематизации и обобщения математических знаний, организации различных видов познавательной деятельности, осуществления прикладной направленности учебного процесса и его деятельностной и личностной ориентации;
• решают проблемы: методологической ориентации обучения математике, реализации межпредметных и внутрипредметных связей, преемственности в учебном процессе; осуществления дифференциации и индивидуализации в обучении;
• определяют развитие: математического мышления, математической культуры обучающихся, самостоятельности, активности личности, а также ее творческих качеств;
• обусловливают формирование: общеучебных умений и способов деятельности, мировоззренческой и мотивационной сфер личности, познавательной и общей культуры обучающихся, широкого круга компетенций.

Рассматривая содержание образования в аспекте повышения эффективности обучения и активности его субъектов, можно говорить о двух его формах, одновременно функционирующих в познавательном процессе: уже освоенное школьником содержание (в форме знаний, умений, способов деятельности, ценностей, мотивов и т.д.), выступающее ресурсом, определяющим эффективность процесса познания, объектом которого, в свою очередь, является предметное содержащее подлежащее освоению. Таким образом, содержание образования одновременно выступает пространством функционирования познавательной активности обучающихся и пространством ее развития. А поскольку само содержание задается нормативными документами и не может быть значительно изменено, то повышение эффективности усвоения предметного содержания можно обеспечить, представив его в форме, которая будет способствовать активизации деятельности обучающихся, то есть в форме задачных систем. Не случайно философское определение понятия «задача» устанавливает ее активизирующий характер, описывая ее как «знание о незнании, возникающее в противоречии между субъектом и объектом, которое может возникнуть при контакте пассивного характера объекта и субъекта. Задача предполагает побуждение к активации такого контакта, образовавшегося внутри или возникшую извне потребность субъекта к устранению обнаруженного им противоречия» [3, с. 46].

При этом содержание, глубина и способы преобразования учебного материала в процессе его усвоения будут определяться учебной ситуацией, обозначенной задачей, а деятельность по решению задач необходимо выстраивать как систему учебных (мыслительных и практических) действий, ориентированных на продвижение школьника в предметном содержании. Сказанное, позволяет указать на общие характеристики задачной системы, ориентированной на активизацию деятельности обучающихся и повышение эффективности учебного процесса. Систему задач можно считать эффективной, если она обеспечивает:

• содержательную основу учебно-познавательной деятельности (представление учебного материала с необходимой полнотой, глубиной и детализацией);
• деятельностную основу процесса познания (возможность широкого варьирования методов и форм учебной работы, возможность практического применения усвоенных знаний, формирования и совершенствования предметных и обобщенных способов деятельности);
• личностно-развивающий компонент обучения (формирование гибкости, глубины мышления, развитие познавательной мотивации, интереса к предмету познания и к самой познавательной деятельности, нравственно-волевых качеств).

Заметим, практическое использования задач в обучении математике в силу ее предметных особенностей имеет свои отличительные черты. Это во многом связано с тем, что учителя математики соотносят понятие задачи исключительно с ее предметным (математическим), а не общедидактическим контекстом. Ограниченное понимание роли и дидактического назначения задач приводит к тому, что задачи в подавляющем большинстве используются на этапе закрепления изученного материала и в рамках контрольных процедур. При этом этап изучения нового материала строится на основе объяснения учителя, а эффективность работы учащихся над задачей, определяется тем, получен ли правильный ответ или нет. Таким образом, потенциал задачного подхода остается нереализованным.

Ранее мы описывали процесс конструирования задачных систем в виде детализации технологической цепочки: целеполагание ‒ дозирование ‒ методическое структурирование [6], особенности конструирования заданий, ориентированных на повышение эффективности групповой работы в обучении математике [7], а также отмечали, что на этапе проектирования урока необходимо осуществлять подбор задач, планирование деятельности по их решению на основе определения их качественных и количественных характеристик, устанавливающих вклад задачи в достижение образовательных целей. В качестве такой системной характеристики задачи была определена ее дидактическую ценность [8].

В данной статье приведем пример, использования системы задач на этапе изучения нового материала и первичного его закрепления, поскольку анализ школьной практики показывает, что именно этот аспект использования задач вызывает затруднение учителей.

Тема урока «Теорема о вписанном угле».

Задача 1. Градусная мера угла КОМ (рисунок 1) равна 76^о. С помощью циркуля и линейки постройте угол 38^о, не проводя биссектрису данного угла.

Комментарий. Задача является достаточно сложной. Работа с данной задачей направлена на формирование способности к анализу, умений видеть проблему, выдвигать гипотезы, проверять их истинность. Школьники предлагают идеи решения задачи. Если учащиеся самостоятельно не могут решить задачу, то учитель не должен явно подсказывать идею решения. Следуя логике задачного подхода, подсказку учащиеся должны получить также в процессе решения задачи, поэтому учитель, прогнозируя возможные затруднения, должен подготовить и предложить вспомогательную задачу.

Задача 2 (вспомогательная). На чертеже (рисунок 2) . Найдите: .

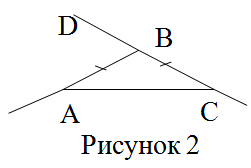Комментарий. При решении вспомогательной задачи учащиеся вспоминают свойства равнобедренного треугольника и теорему о внешнем угле треугольника. Найденные углы фиксируются на чертеже. Школьники, работая по чертежу, находят нужные углы и замечают, что величина угла АВD в два раза больше величин углов ВАС и АСВ. Затем учитель предлагает еще раз проанализировать условие задачи 1 и выдвинуть идею ее решения. Школьники самостоятельно записывают решение и затем устно могут доказать, что найденные углы удовлетворяют требованию задачи.

Задача 3. Назовите и охарактеризуйте фигуры, которые вы видите на чертеже (рисунок 3).

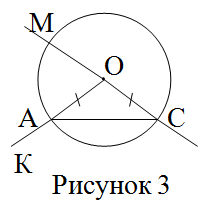Комментарий. Организация поисковой деятельности учащихся направлена на «открытие» теоремы. При этом доказательство одного из ее частных случаев учащимися выполняется в ходе этого «открытия». Это позволяет в дальнейшем самостоятельно его воспроизвести. Учитель добивается того, чтобы учащиеся давали подробные характеристики элементам чертежа, обосновывая свои утверждения. Работу с задачей целесообразно закончить формулированием теоремы о величинах вписанного и центрального углов.

Задача 4. Мы сформулировали утверждение о величинах центрального и вписанного углов для случая, когда сторона вписанного угла проходит через центр окружности. Справедливо ли утверждение для любых вписанных углов?

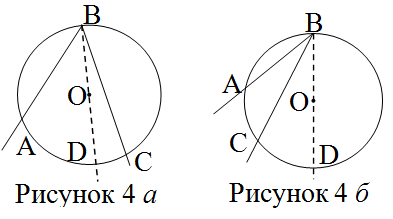Комментарий. Учитель при необходимости задает наводящие вопросы, добиваясь того, чтобы школьники на доске или в тетрадях изобразили несколько чертежей с различным расположением сторон вписанного угла относительно центра окружности и сделали вывод, что, кроме ранее рассмотренного случая, когда центр окружности лежит на стороне угла, возможны еще два различных случая, когда центр окружности лежит: внутри вписанного угла или вне вписанного угла. Идею доказательства школьники находят, опираясь на ранее рассмотренный случай и дополнительное построение (луч, выходящий из вершины вписанного угла и проходящий через центр окружности (рисунки 4, а, 6).

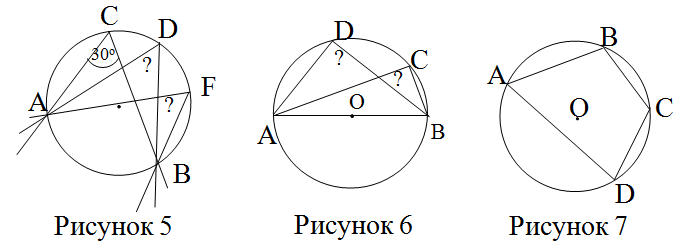
Задача 5. Мини-исследование. Найдите неизвестные углы, сформулируйте и докажите соответствующие следствия из теоремы (для первого варианта рисунок 5, для второго ‒ 6).

Комментарий. Представители каждого из вариантов, выступают с результатами своего исследования, объясняют свое решение у доски, формулируют и доказывают полученное следствие из изученной теоремы.

Задача 6 (исследовательская домашняя работа). В окружность вписан четырехугольник (рисунок 7). Исследуйте свойство углов этого четырехугольника. Сформулируйте полученное свойство (обязательное задание). Сформулируйте обратное утверждение и докажите его (задание повышенной сложности).

Комментарий. Выполняя исследование в рамках домашней работы, учащиеся выходят на новую проблемы, решая которую самостоятельно выявляют свойство вписанного четырехугольника.

Работу с системой задач целесообразно заканчивать фазой рефлексии. В данном случае рефлексию можно провести в два этапа: в конце урока и в начале следующего урока, после выполнения домашней исследовательской работы. Обсуждая работу учащихся нужно не только останавливаться на том, что понравилось или что изучили, гораздо важнее, чтобы школьники осознали как они пришли к такому результату, что помогло им «открыть» теорему, доказать ее, получить следствия. Именно осознание собственной мыслительной деятельности во многом обеспечивает формирование у обучающихся «путей мышления» [5].

Разрабатывая подобные задания необходимо точно представлять, какие задачи взять за основу задания, как организовать работу с ними, чтобы натолкнуть школьников на нужный математический факт. Учитывая индивидуальные качества учеников, задание можно детализировать вопросами, которые будут служить своего рода подсказкой или напротив – какие-то элементы задания удалить, повышая его сложность Примечательно также то, что, как показывает практика, подобные задачные системы легко адаптируются для групповой или индивидуальной работы.

В контексте вышесказанного становится очевидным, что при реализации задачного подхода планирование уроков не должно ограничивается подбором задач из школьных учебников, задачников или каких-либо других источников и выстраиванием их в определенном порядке. Любые задачи или даже задачные системы, сконструированные не самим учителем, не всегда могут быть успешно им применены в конкретной познавательной ситуации. Задачная система, используемая на уроке должна учитывать отличительные особенности класса, индивидуальные способности и качества отдельных учащихся, а также личностные и профессиональные качества учителя.

Задачи (системы задач), представленные в пособиях могут послужить лишь каркасом для той задачной структуры, которая станет основой урока. Задачи этой структуры должны быть обеспечены системой дополнительных требований, вопросов, указаний и т.п., которые будут определять не только предметную, но и метапредметную познавательную деятельность во всем многообразии ее форм, методов и средств, а также реализовывать целостность процесса познания через обеспечение широкого спектра связей (предметных, межпредметных, логических, структурных, функциональных, эмоциональных и т.д.). Именно это позволит в полной мере реализовать положения задачного подхода: выстроить процесс обучения как деятельность по решению разнообразных задач на любом этапе изучения, закрепления и обобщения учебного содержания, минимизировав монологическую речь учителя и обеспечив функционирование обучающихся на потенциальном уровне интеллектуально-личностных возможностей и стратегической самостоятельности.

1. Балл Г. А. Теория учебных задач: Психолого-педагогический аспект. М.: Педагогика, 1990. 184 с.
2. Блинов В.М. Эффективность обучения: методологический анализ определения этой категории в дидактике. М.: Педагогика, 1976.192 с.
3. Краткая философская энциклопедия. Сост.: Е. Ф. Губский, Г. В. Кораблева, В. А. Лутченко. М.: Прогресс, 1994. 576 с.
4. Темняткина О. В. ,  Токменинова Д. В.  Современные подходы к оценке эффективности работы учителей //Вопросы образования. 2018. № 3. С. 180-195.
5. Чуприкова Н. И. Умственное развитие: принцип дифференциации. СПб.: Питер, 2007. 448 с.
6. Шмигирилова И. Б. Особенности конструирования учебно-поисковых заданий в компетентностном обучении математике // Наука и школа. 2017. № 3. С. 152-160.
7. Шмигирилова И. Б. Особенности конструирования заданий, ориентированных на повышение эффективности групповой работы // Актуальные проблемы обучения математике и информатике в школе и в вузе: Материалы IV Международной научной конференции. Т.1. М.: МПГУ, 2018 г. С. 262-266.
8. Шмигирилова И. Б. Дидактическая ценность задачи и пути ее повышения // Наука и школа. 2018. № 6. С. 130-135.
9. Boylan М., Maxwell В., Wolstenholme С., Jay Т, Demack S. The Mathematics Teacher Exchange and ‘Mastery’ in England: The Evidence for the Efficacy of Component Practices Education Sciences 2018, 8 (202). doi:10.3390/educsci8040202